CUDA Tutorial: Implicit Matrix Factorization on the GPU

I recently bought a system that actually has a decent GPU on it, and I thought it would be cool to learn a little bit about CUDA programming to really take advantage of it.

The obvious choice of problems to get started with was extending my implicit matrix factorization code to run on the GPU. I’ve written a couple of posts about this recommendation algorithm already, but the task is basically to learn a weighted regularized matrix factorization given a set of positive only implicit user feedback. The nice thing about this model is that it is relatively simple while still not being possible to express efficiently on higher level frameworks like TensorFlow or PyTorch. It’s also inherently embarrassingly parallel and well suited for running on the GPU.

This post aims to serve as a really basic tutorial on how to write code for the GPU using the CUDA toolkit. I found that CUDA programming was pretty interesting, but it took me a little bit to learn how to do this effectively - and I wanted to share what I learned while it is still fresh in my mind.

The cool thing about processing on the GPU is that this CUDA code is significantly faster than the equivalent code running on the CPU. As an example, look at the training times when run on the MovieLens 20M dataset:

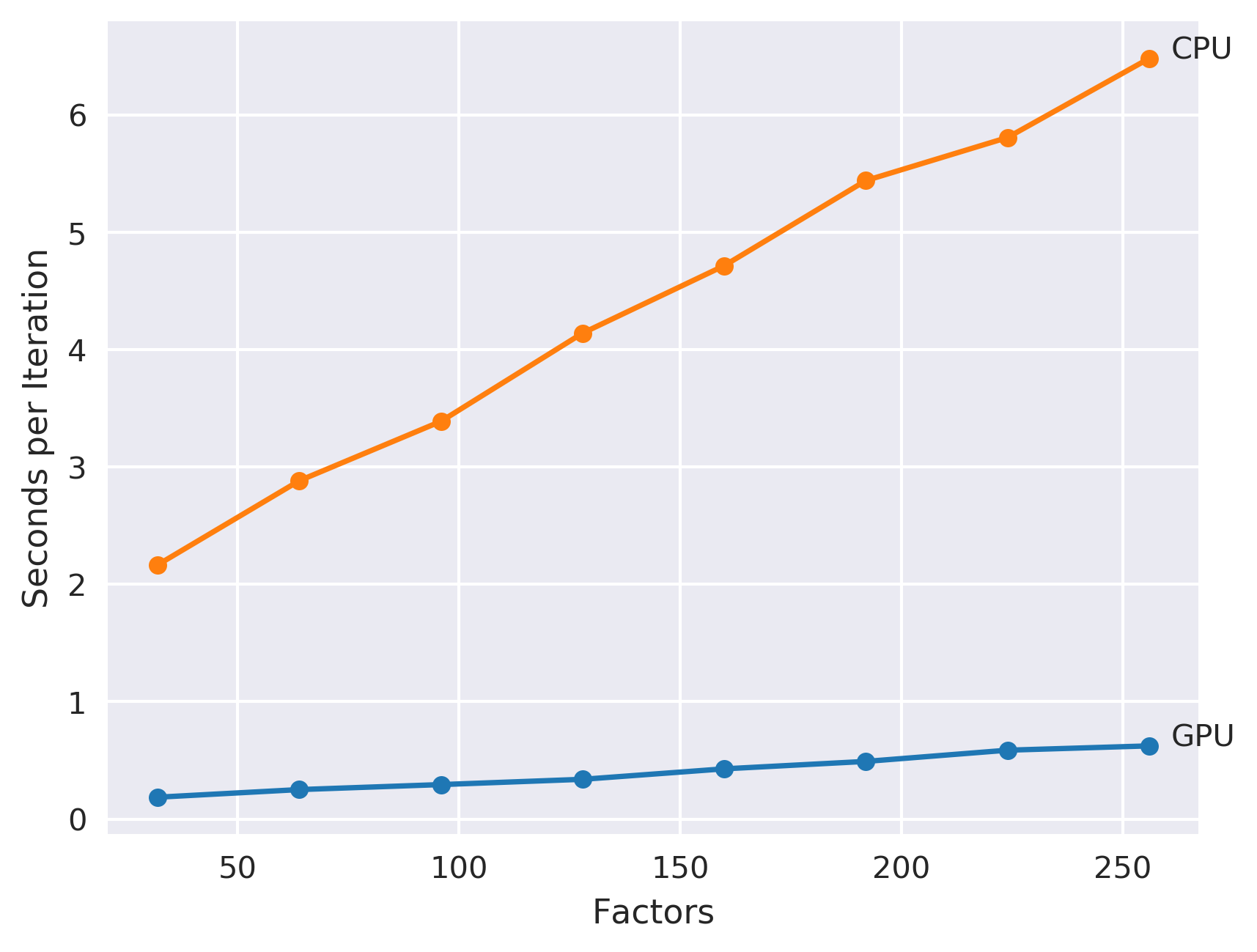
For the 256 factor model, the GPU version is roughly 8 times faster than the equivalent code running on the CPU, and is 68 times faster than the equivalent model included in Spark MLlib!

CUDA Programming Basics

There are a couple major differences in the programming model when targeting GPU’s, which are reflections on the underlying hardware differences.

Each GPU contains a number of Streaming Multiprocessors (SM) with each SM running a number of threads. For example, my graphics card has 28 SM’s which can each run 128 threads in parallel - meaning there are 3584 total CUDA cores. These threads are grouped into warp’s of 32 threads each - with the critical piece of info being that each thread in a warp runs exactly the same instruction at the same time. This model is named Single Instruction Multiple Thread (SIMT) and is conceptually similar to SIMD instructions on CPU’s - but is substantially more flexible.

The other major hardware difference is in the memory model. Each GPU has a certain amount of dedicated DRAM on the device. For instance, on my GPU there is 11GB of RAM to use. This memory is global and can be accessed by every Streaming Multiprocessor on the device, but the downside is that its the slowest memory to access. GPU’s also have a limited amount of shared memory that is shared among threads in an SM. Shared memory is on the same chip as the SM, meaning that it is both much faster and there is much less of it. Finally, each thread has a set of registers that can hold data locally.

To access this hardware model, NVIDIA has supplied a custom nvcc compiler as part of its CUDA toolkit. This acts as a C/C++ compiler like gcc or llvm - with a couple of custom extensions for writing code for the GPU.

For example, to launch a simple kernel on the GPU you could go like:

l2_regularize_kernel&lt&lt&ltblock_count, thread_count&gt&gt&gt(factors, regularization, YtY);

The <<< and >>> symbols tell nvcc that the host CPU is calling a kernel function that should run on the GPU device. The first parameter inside these symbols is the number of blocks of threads to run, where each block will get run on a single SM. The second parameter specifies the number of threads that run inside this block.

The kernel code itself is denoted by the __global__ keyword and looks like:

__global__
void l2_regularize_kernel(int factors, float regularization, float * YtY) {
    int index = blockIdx.x * blockDim.x + threadIdx.x;
    if (index < factors) {
        YtY[index * factors + index] += regularization;
    }
}

Inside of the kernel, there are special variables blockIdx and threadIdx that indicate what block and thread are currently being run. There are also blockDim and gridDim variables that indicate how many threads and how many blocks exist as well. These variables are triplets of x/y/z dimensions, but for the purposes of this post I’m only using the x dimension.

With this specific kernel, each thread is updating a single value along the diagonal of a square matrix YtY - in order to add [L2 regularization](https://en.wikipedia.org/wiki/Regularization_(mathematics) to this matrix factorization model. This is done in parallel - and the work is divided by the index variable according to which block/thread is being run and how many threads are in each block.

Matrix Factorization Strategy

My idea was to basically port the conjugate gradient solver code over to run on the GPU.

Because of SIMT processing, the key to getting good results is making sure that we minimize data dependent conditionals across threads in a warp. Since I’m processing sparse data, there can be a variable number of items per user - and if threads were processing different users there could be frequent stalls.

So the idea here is that each block will calculate a factor vector for a single user, and each thread in that block will calculate a single value of that vector.

While this sounds complicated, the resulting code is actually pretty simple and easy to read. For instance here is the section of code that does the Conjugate Gradient update step in CUDA:

// standard CG update
float alpha = rsold / dot(p, Ap);
x[threadIdx.x] += alpha * p[threadIdx.x];
r[threadIdx.x] -= alpha * Ap[threadIdx.x];
float rsnew = dot(r, r);
p[threadIdx.x] = r[threadIdx.x] + (rsnew/rsold) * p[threadIdx.x];

This compares pretty well to the pure python version:

# standard CG update
alpha = rsold / p.dot(Ap)
x += alpha * p
r -= alpha * Ap
rsnew = r.dot(r)
p = r + (rsnew / rsold) * p

And is much more readable than the equivalent code written in Cython.

The only tricky part here is the dot product calculation. This requires summing values amongst threads - which leads to some coordination problems.

Parallel Reductions

My original version of the dot product code looked like this:

__inline__ __device__
float dot(const float * a, const float * b) {
    __syncthreads();

    __shared__ float ret;
    if (threadIdx.x == 0) {
        ret = 0;
    }
    __syncthreads();

    // The vast majority of time is spent in the next 'atomicAdd' line
    atomicAdd(&ret, a[threadIdx.x] * b[threadIdx.x]);
    __syncthreads();
    return ret;
}

It basically summed up the values in shared memory using the CUDA atomicAdd instruction. The __syncthreads() calls instruct the GPU to wait until every thread has reached that line - while each warp of threads only executes the same instruction, inside a thread block multiple warps can be running so its necessary to synchronize before they start modifying shared memory. The __device__ directive indicates to the compiler that this code will run on the GPU, and be called by other code running on the GPU.

While this code works - using atomicAdd like this is not particularly fast. When looking for ways to improve this code, I found a post showing how to speedup these parallel reductions using the ‘Shuffle’ instructions that were added with Kepler GPU’s.

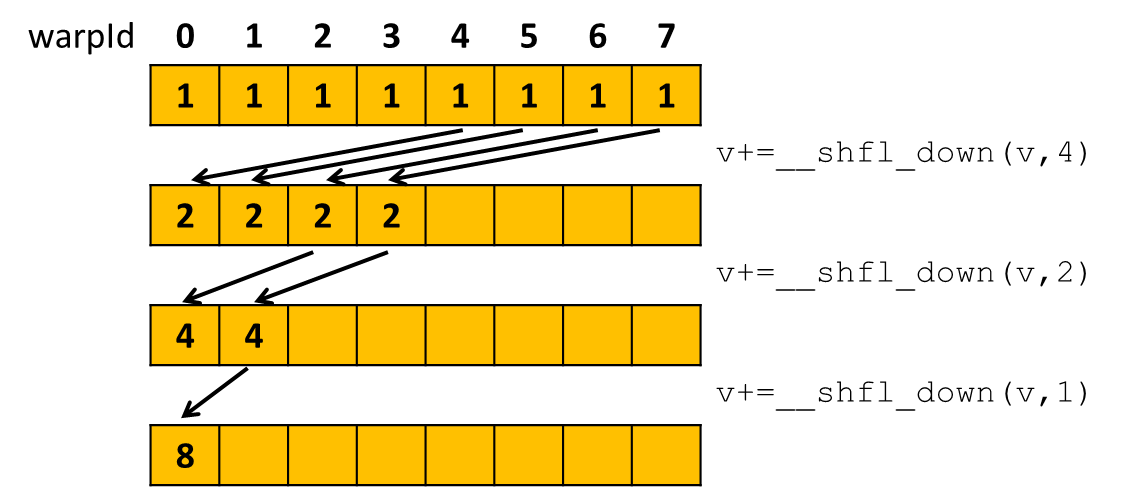
Shuffle instructions let you share data in amongst threads in a warp. For example, the __shfl_down_sync instruction takes a value and an offset as parameters. The value passed in is shuffled down to other threads in the warp - with the offset giving how far it’s passed. So the idea is to use this instruction to form a reduction tree to sum up the values:

From devblogs.nvidia.com/parallelforall

The code to sum up values in a warp looks like:

__inline__ __device__
float warp_reduce_sum(float val) {
    unsigned int active = __active_mask();
    #pragma unroll
    for (int offset = WARP_SIZE / 2; offset > 0; offset /= 2) {
        val += __shfl_down_sync(active, val, offset);
    }
    return val;
}

To compute the dot product over the entire thread block, the idea is to reduce each warp of 32 threads using the warp_reduce_sum function - and then store the results in shared memory and reduce again:

__inline__ __device__
float dot(const float * a, const float * b) {
    __syncthreads();
    static __shared__ float shared[32];

    // figure out the warp/ position inside the warp
    int warp =  threadIdx.x / WARP_SIZE;
    int lane = threadIdx.x % WARP_SIZE;

    // partially reduce the dot product inside each warp using a shuffle
    float val = a[threadIdx.x] * b[threadIdx.x];
    val = warp_reduce_sum(val);

    // write out the partial reduction to shared memory if appropriate
    if (lane == 0) {
        shared[warp] = val;
    }
    __syncthreads();

    // if we we don't have multiple warps, we're done
    if (blockDim.x <= WARP_SIZE) {
        return shared[0];
    }

    // otherwise reduce again in the first warp
    val = (threadIdx.x < blockDim.x / WARP_SIZE) ? shared[lane] : 0;
    if (warp == 0) {
        val = warp_reduce_sum(val);
        // broadcast back to shared memory
        if (threadIdx.x == 0) {
            shared[0] = val;
        }
    }
    __syncthreads();
    return shared[0];
}

Computing the dot product like this led to a 15% speed up in total processing time. While this is a respectable improvement, there were other much more major gains still to be had.

Speeding things up: Memory Coalescing

Another hotspot I found was when doing a matrix-vector multiplication - which I originally wrote like this:

// multiply the YtY matrix by X
float temp = 0;
for (int i = 0; i < factors; ++i) {
    temp += x[i] * YtY[threadIdx.x * factors + i];
}

The problem with that code is in accessing the values of the YtY matrix. While its correct for a basic matrix multiplication, it caused a lot of global memory accesses - that weren’t aligned across the threads in the warp. Since this YtY matrix is symmetric, we can coalesce these memory accesses so that each thread is reading adjacent values:

float temp = 0;
for (int i = 0; i < factors; ++i) {
    temp += x[i] * YtY[i * factors + threadIdx.x];
}

This simple change more than doubles the processing speed of the whole algorithm! This article has more details on why this matters.

Putting it all together

I’ve added this code to my implicit recommendations library - it should automatically pick up if you have a CUDA compiler and can be easily enabled from python by setting the use_gpu flag when constructing the model.

I’ve put all the core CUDA code for this algorithm below. While it took a while to learn everything I need to write this - I think the code itself is pretty simple:

__global__
void least_squares_kernel(int factors, int user_count, int item_count, float * X,
                          const float * Y, const float * YtY,
                          const int * indptr, const int * indices, const float * data,
                          int cg_steps) {
    // Ap/r/p are vectors for CG update - use dynamic shared memory to store
    // https://devblogs.nvidia.com/parallelforall/using-shared-memory-cuda-cc/
    extern __shared__ float shared_memory[];
    float * Ap = &shared_memory[0];
    float * r = &shared_memory[factors];
    float * p = &shared_memory[2*factors];

    // Stride over users in the grid:
    // https://devblogs.nvidia.com/parallelforall/cuda-pro-tip-write-flexible-kernels-grid-stride-loops/
    for (int u = blockIdx.x; u < user_count; u += gridDim.x) {
        float * x = &X[u * factors];

        // calculate residual r = YtCuPu - YtCuY Xu
        float temp = 0;
        for (int i = 0; i < factors; ++i) {
            temp -= x[i] * YtY[i * factors + threadIdx.x];
        }
        for (int index = indptr[u]; index < indptr[u + 1]; ++index) {
            const float * Yi = &Y[indices[index] * factors];
            float confidence = data[index];
            temp += (confidence - (confidence - 1) * dot(Yi, x)) * Yi[threadIdx.x];
        }
        p[threadIdx.x] = r[threadIdx.x] = temp;

        float rsold = dot(r, r);

        for (int it = 0; it < cg_steps; ++it) {
            // calculate Ap = YtCuYp - without actually calculating YtCuY
            Ap[threadIdx.x] = 0;
            for (int i = 0; i < factors; ++i) {
                Ap[threadIdx.x] += p[i] * YtY[i * factors + threadIdx.x];
            }
            for (int index = indptr[u]; index < indptr[u + 1]; ++index) {
                const float * Yi = &Y[indices[index] * factors];
                Ap[threadIdx.x] += (data[index] - 1) * dot(Yi, p) * Yi[threadIdx.x];
            }

            // standard CG update
            float alpha = rsold / dot(p, Ap);
            x[threadIdx.x] += alpha * p[threadIdx.x];
            r[threadIdx.x] -= alpha * Ap[threadIdx.x];
            float rsnew = dot(r, r);
            p[threadIdx.x] = r[threadIdx.x] + (rsnew/rsold) * p[threadIdx.x];
            rsold = rsnew;
        }
    }
}

void CudaLeastSquaresSolver::least_squares(const CudaCSRMatrix & Cui,
                                           CudaDenseMatrix * X,
                                           const CudaDenseMatrix & Y,
                                           float regularization,
                                           int cg_steps) const {
    int item_count = Y.rows, user_count = X->rows, factors = X->cols;
    if (X->cols != Y.cols) throw invalid_argument("X and Y should have the same number of columns");
    if (X->cols != YtY.cols) throw invalid_argument("Columns of X don't match number of factors");
    if (Cui.rows != X->rows) throw invalid_argument("Dimensionality mismatch between Cui and X");
    if (Cui.cols != Y.rows) throw invalid_argument("Dimensionality mismatch between Cui and Y");

    // calculate YtY: note this expects col-major (and we have row-major basically)
    // so that we're inverting the CUBLAS_OP_T/CU_BLAS_OP_N ordering to overcome
    // this (like calculate YYt instead of YtY)
    float alpha = 1.0, beta = 0.;
    CHECK_CUBLAS(cublasSgemm(blas_handle, CUBLAS_OP_N, CUBLAS_OP_T,
                             factors, factors, item_count,
                             &alpha,
                             Y.data, factors,
                             Y.data, factors,
                             &beta,
                             YtY.data, factors));
    CHECK_CUDA(cudaDeviceSynchronize());

    // regularize the matrix
    l2_regularize_kernel&lt&lt&lt1, factors&gt&gt&gt(factors, regularization, YtY.data);
    CHECK_CUDA(cudaDeviceSynchronize());

    int block_count = 1024;
    int thread_count = factors;
    int shared_memory_size = sizeof(float) * (3 * factors);

    // Update factors for each user
    least_squares_cg_kernel&lt&lt&ltblock_count, thread_count, shared_memory_size&gt&gt&gt(
        factors, user_count, item_count,
        X->data, Y.data, YtY.data, Cui.indptr, Cui.indices, Cui.data, cg_steps);

    CHECK_CUDA(cudaDeviceSynchronize());
}

I’ve linked to about 4 different posts here in NVIDIA’s Parallel ForAll Blog - I highly recommend checking it out if this post is interesting to you all. Also, the CUDA C Programming Guide contains a bunch of great information.